Interesting Facts About Parabolas

In this post, we will explore point-directrix parabolas with in a bit more depth, although with less rigor. I won't prove anything below, but I will give some justification for why you should believe me, which will allow you to prove it on your own if you are so inclined. We starting with the following interesting fact:

Fact 1: Start with any circle. Choose a directrix line that is tangent to that circle, and a focus point on that circle. Then:

• If the focus point is on the directrix line, then the line perpendicular to the directrix line and passing through the focus point will pass through the center of the circle.
• If the focus point is not on the directrix line, then the parabola formed by the focus point and directrix line will pass through the center of the circle.

A picture is worth a thousand words, so here is what I mean:

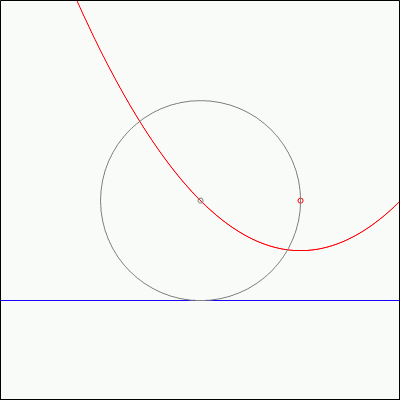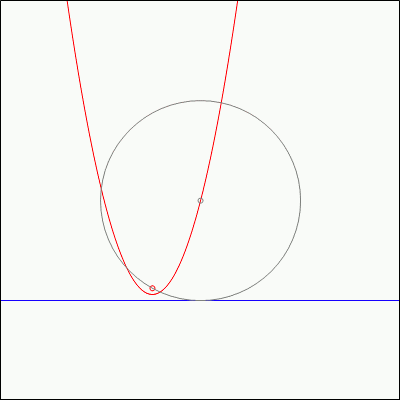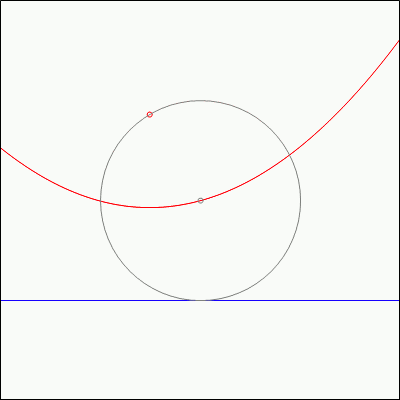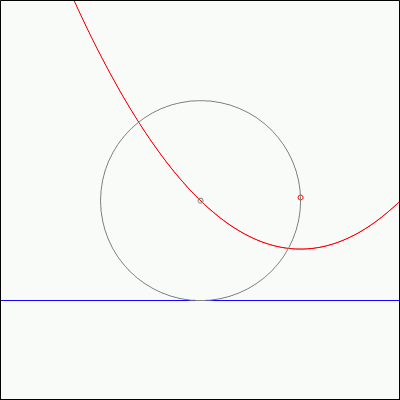
This interesting fact, while interesting, is not much of a surprise. Recall that the parabola is defined as the set of points which are the same distance away from the directrix line and the focus point. Therefore, if you draw a circle centered at a point on the parabola and passing through the focus point, it will turn out to be tangent to the directrix line. Fact 1 just does this backwards by starting with the circle, and then drawing the parabola generated from one of the points on the circle.

Things get a bit more interesting when we pick more than one focus point:

This image shows another interesting fact:

Fact 2: Start with any circle. Choose a directrix line that is tangent to that circle, and two distinct focus points on that circle. Then the parabolas formed by the directrix and each focus point intersect at the center point of the circle. (Special case: If one of the focus points is on the directrix line, then the perpendicular bisector of the directrix line passing through that focus point will intersect the other parabola at the center of the circle.)

This is another interesting, but unsurprising fact. The center of the circle, by construction, is the same distance from both focus points and the directrix. That last sentence sounds kind of like the definition of the bisector of two points, which leads us to a third interesting fact:

Fact 3: Take any directrix line, and two distinct focus points not on the directrix line. Any intersection point of the parabolas formed by each focus point and the directrix will lie on the bisector of the focus points.

This fact only puts restrictions on the point or points of intersection if they exist:

• If the focus points are on opposite sides of the directrix line, then the parabolas will not intersect: any circle containing those focus points would cross the directrix line, not be tangent to it.
• If the focus points are the same distance away from the line, then the parabolas will only intersect at a single point.

Here is a picture demonstrating Fact 3:

Fact 3 gets a lot more intersting when, instead of animating one of the focus points, we animate the directrix line:

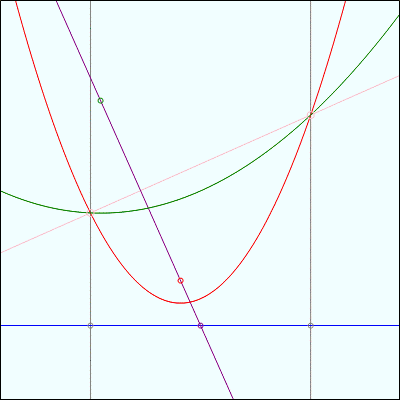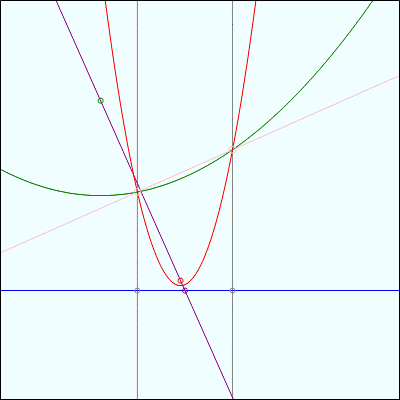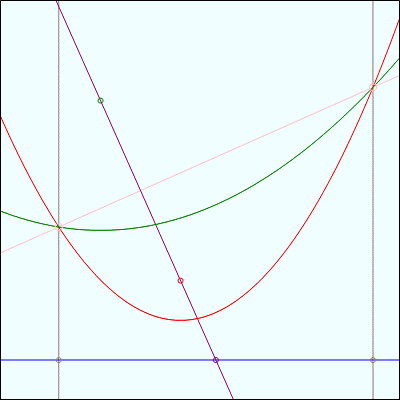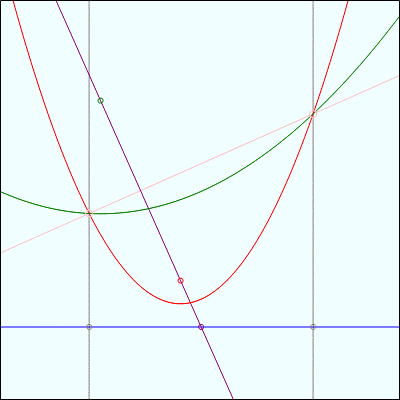
Here, the two intersection points of the parabolas are tracing along a stationary bisector. In both images, note also that the closest point on the directrix to each intersection point is the same distance away from the intersection point of the directrix and the line containing both focus points.

There is one more interesting fact to go over in this post, although it is more of a corollary to Fact 2, so we won't give it its own number: if you take a circle, and a directrix line tangent to the circle, and three distinct focus points on the circle that aren't on the directrix line, then all three parabolas intersect at the center of the circle.

On its own, this is not very interesting; we're just doing Fact 2 again with another focus point, and nothing is stopping us from picking, say, nineteen focus points and intersecting all of those parabolas.

What we are going to want to do soon, however, is the reverse operation: given three focus points, we want to find a directrix line such that the parabolas formed by each focus point and the directrix line intersect at a single point. The previous paragraph suggests an algorithm: find a circle containing all three points, and then we can choose any directrix line we wish that is tangent to that circle. This algorithm will also tell us the point of intersection; it is the center of the circle.

How can we find a circle containing three distinct points, though? Tune in next time to find out.